
Did you know that there are four different types of sentences and that these sentences help us to define propositional logic?

Jenn, Founder Calcworkshop ® , 15+ Years Experience (Licensed & Certified Teacher)
And the sentences we are most interested in are declarative!
Because propositions, also called statements, are declarative sentences that are either true or false, but not both. This means that every proposition is either true (T) or false (F).
Let’s look at a few examples of how we determine the type of sentence illustrated, and if it is a proposition, we will identify its truth value.

Proposition In A Sentence
Notice for our last two examples, that while the sentences are declarative, they are not a proposition because we don’t know the value of “she” or “x” or “y” — hence, we are unable to determine the truth value for the sentence.
These types of scenarios are called paradoxes and open sentences, respectively.
A paradox is a declarative sentence that is true and false at the same time — thus, a paradox is not a proposition. Consequently, for the example above, when we say “she walks to school,” this is considered a paradox because since we don’t know who “she” is, we can’t identify the truth of this statement.
An open sentence is also declarative but is not a proposition because it contains one or more variables whose truth or falsity depends on the values of these variables. Notice for the example above where say |x+y| < |x| + |y|, because we are unsure of what x or y represent. Once again, we cannot identify the truth or falsehood — hence, this sentence is not a proposition.
Now, just like we see with numbers and operations like addition, subtraction, multiplication, and division, we are interested in how statements can be combined to produce new statements as discussed by Stanford University.
The combination of simple statements using logical connectives is called a compound statement, and the symbols we use to represent propositional variables and operations are called symbolic logic.
Throughout our study of discrete mathematics, we will be given propositional statements that form an argument as we will then need to decide whether the given argument is valid or not. We will extract symbols and perform calculations, just like we would in algebra, and ultimately reach a conclusion based on our results.
So what are some of the common connective symbols and statements found in discrete math?

What is extremely important to emphasize and point out is that the negation of a statement will always have the opposite truth value compared with the original statement.
For example, let’s suppose we have the statement, “Rome is the capital of Italy.” This is a true propositional statement. Therefore, the negation of this statement, “Rome is not the capital of Italy,” must be false.
With compound statements, the ability to determine its truth value can be a little more complicated.
Thankfully, a truth table is a fantastic way to determine the truth or falsehood of a compound statement based on its components’ truth values.
We follow the 2 to the n rule and the lexicographic ordering.
The 2-n rule says that if we have n number of unique variables, then the number of rows in the table will be 2 to the nth power. For example, if we have two individual variables, then there will be four rows because 2 to the second power is 4, and if there are three unique variables, then there will be eight rows because 2 to the 3rd power is 8.
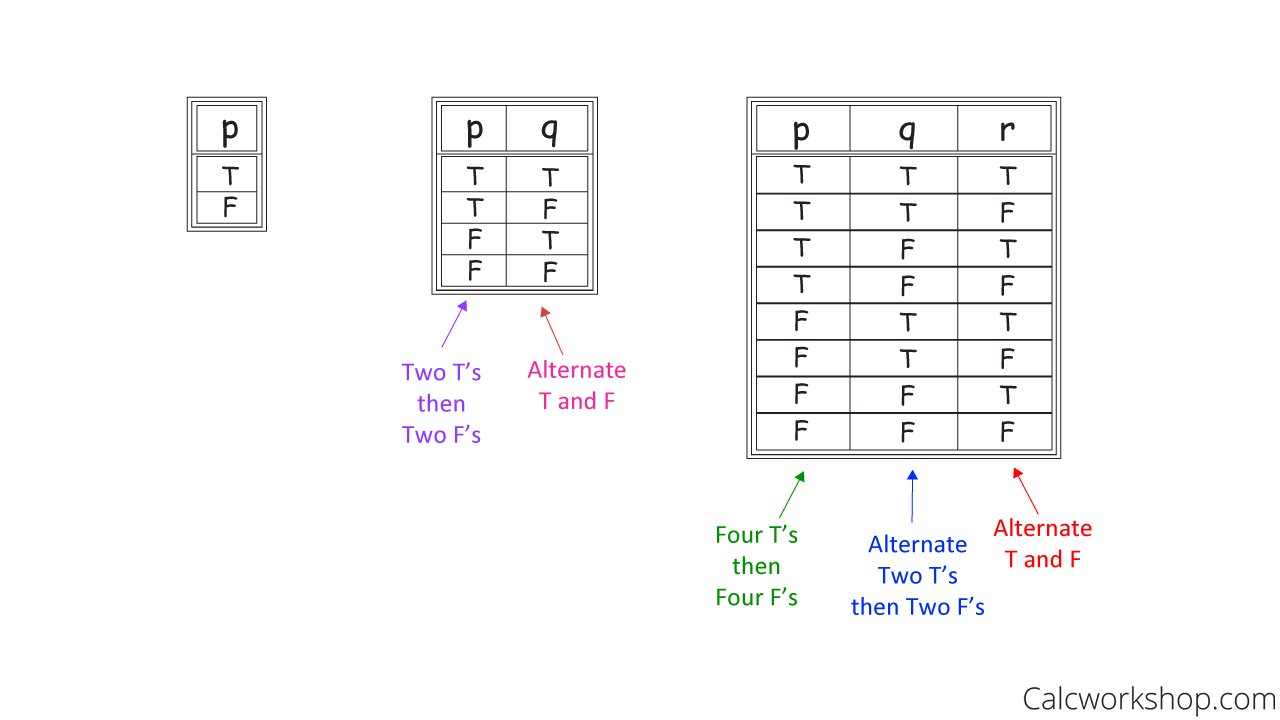
Constructing Truth Tables
Now the lexicographic ordering is a pattern that helps us to put values in order to make it easier to compare. To help us understand the importance of order, let’s start with an example. Assume you have a fair coin, and you flip it twice. This means that you can get the following results:
This gives us four possibilities.
Therefore, we must account for all possible scenarios when we construct our tables to help keep our options straight and organized (so we never forget anything) — we follow this simple pattern.
Now let’s see a truth table in action.
What is the truth value of “I will make you supper, and I will make your dessert.”
Now the fact of the matter is that people are notorious for making a promise that they don’t always keep. Yes, it’s sad but true. Therefore, our truth table must account for all possible scenarios.

Truth Tables Conjunction
Notice that for an “and” statement, we will only have a “true” value when both p and q are both true.
Now, using the same propositional statements, let’s now suppose we want to find the truth value for “I will make you supper, or I will make your dessert.”
This means that for an “or” statement, we will only get a “false” value when p and q are both false.

Throughout this lesson, we will learn how to identify propositional statements, negate propositions, understand the difference between the inclusive or and the exclusive or, translate propositions from English into symbolic logic and vise-versa, and construct truth tables for various scenarios and begin to develop the idea of logical equivalence.
Let’s get to it!
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.